Personal page of Eduard I. Vatutin

Main page | Cribs | Humor | For students | OEIS

Eduard I. Vatutin
Personal page
(russian version)

Professor of department of Computer sciences of Southwest State University, Kursk, Russia
Candidate of technical sciences, speciality 05.13.05 "Elements and devices of computer facilities and control systems", 2009
Microsoft Certified Professional (MCP), exam 70-290 "Managing and Maintaining a Microsoft Windows Server 2003 Environment", 2007

Areas of interest:

programming (Delphi, Assembler, C++);

parallel programming (vector extensions, CUDA);

low-level micro-architectural software optimization for SIMD-extensions for x86 processors family (MMX, SSE, ...);

getting separations of parallel logic control algorithms during logic multicontrollers design;

equivalent transformations and numerical estimations of graph-schemes of parallel algorithms;

hardware oriented accelerators and coprocessors design;

combinatorics, combinatorial optimization, heuristic methods for discrete combinatorial optimization problems solving;

graphs theory;

grid-systems (volunteer computing), BOINC;

diagonal Latin squares;

digital photo;

alternative history;

history of science.

WWW: http://evatutin.narod.ru
e-mail: evatutin (at) rambler (dot) ru
Skype: evatutin
Wiki: evatutin
Блог: evatutin

Tests

Hyper-Threading Tests — testing of Hyper-Threading technology using threads with code of different type (Mem, Int, FPU, SSE). Download (212 KB)

Single Double Extended — determining of effectiveness of FP-operations with different precision (Delphi 7). Download (binary) (41 KB), Download (sources) (2 KB), forum

CUDA base parameters — determining of GPU base parameters. Download (121 KB)

CUDA memory bandwidth — determining of bandwidth of RAM-GPU interconnect. Download (278 KB), forum, results

CUDA matrix multiplication — determining of performance of CPU и GPU during 2048x2048-element matrices multiplication. Download (216 KB), forum, results

Diagonal Latin squares editor — Download (248 KB)

Diagonal Latin squares crossword — crossword based on diagonal Latin squares (like a Sudoku). Download (228 KB)

Direct orthogonal diagonal Latin squares search — program for search of orthogonal diagonal Latin squares (mates) without transversals using. Download (20 KB), announcement

DLS lists

Canonical forms of all main classes of ODLS of orders 1—8 (22 KB) // Announcement, May 04 2020.
Canonical forms of all main classes of ODLS of order 9 (2,6 MB) // Announcement, Dec 07 2020.
Canonical forms of known main classes of ODLS of order 9 (243 MB) // Announcement, Mar 31 2021.
Canonical forms of all main classes of ESODLS of orders 1—8 (2 KB) // Announcement, May 03 2020.
Canonical forms of all main classes of ESODLS of order 9 (611 KB) // Announcement, Dec 07 2020.
Canonical forms of all main classes of SODLS of orders 1—10 (1,4 MB) // Announcement, May 04 2020.
Canonical forms of all main classes of DSODLS of orders 1—10 (5 KB) // Announcement, May 03 2020.

Science

Each formula included in the book to halve the number of buyers.

Stephen Hawking

FERROFLUIDS PHISICS
$\150dpi p_3 = I_s(T_3) \cdot V$
$\150dpi C' = \frac {p_{3}H_{3}} {k T_3 \sinh \frac {p_3 H_3} {k T_3} }$
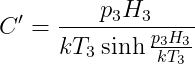
$\150dpi f(\theta) = C' e^ {\left[ \frac {p_3 H_3 \cos \theta} {k T_3} \right]} \sin \frac {\theta} {2}$
$\150dpi \widetilde{H} = H_m \sin \omega t$
$\150dpi F' = I_s H_m \sin (\psi - \alpha + \mu )$
$\150dpi \delta ' = \arctan \frac { \omega \beta } { F'}$
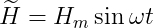
$\150dpi M' = 2K_1 \cos 2 \alpha + I_s H_0 \cos (\psi - \alpha) + \xi E_z \lambda_c^2 \sin ^2 2 \alpha \cos ^4 \beta_3$
$\150dpi \varphi_0 = \frac {F'} {M' \cos \delta ' + \omega \beta \sin \delta '}$
$\150dpi \varphi = \varphi_0 \sin \left( \omega t - \delta ' \right)$
$\150dpi B = \frac {I_s H_0} {2 K_1} \sin \psi, C = \frac {I_s H_0} {2 K_1} \cos \psi$
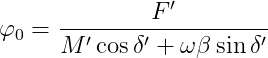
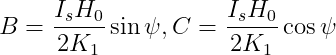
$\150dpi x^4 - 2Bx^3 - (B^2 + C^2 - 1)x^2 - 2Bx - B^2 = 0$
$\150dpi \alpha = \arcsin x$
$\150dpi \varepsilon _{mech} = \lambda _c \sin 2 \alpha \cos ^2 \beta_3 \cdot \varphi$
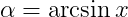
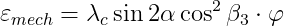
$\150dpi \left \langle \varepsilon _{mech} \right \rangle = \int_{\theta} f (\theta) \varepsilon _{mech} d \theta$
$\150dpi \Delta = a \left( \frac {1} {\sqrt[3]{\varphi}} - 1 \right)$
$\150dpi S_m = \frac{ a^2 \left( 1 + \xi \right) } {\left( a + \Delta \right) ^2 } S_0$
$\150dpi S_z = S_0 - S_m$
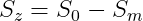
$\150dpi \varepsilon _ {||} \left( \overrightarrow{n} ^ \sigma \right) = \frac { \left \langle \varepsilon _ {mech} \right \rangle E_m S_m } {E_m S_m + E_z S_z}$
$\150dpi \lambda_k = \varepsilon _ {||} \left( \overrightarrow{n} ^ \sigma \right) \frac {al} {a + \Delta} \left(1 - \frac {\mu_{||}}{2} \right)$
1. Vatutin E.I., Chevychelov S.Yu., Rodionov A.A., Ignatenko N.M. Some results of modeling the generation of elastic waves by an alternating magnetic field in magnetically ordered composites (in Russian) // Welding and related technologies in mechanical engineering and electronics. Kursk, 2002, P. 175–182. Download (305 KB)
2. Vatutin E.I., Chevychelov S.Yu., Rodionov A.A., Ignatenko N.M. Modelling of processes of generation of elastic waves by an alternating magnetic field in a thin layer of magnetically disperse systems with a dielectric liquid and solid matrices (in Russian) // The action of electromagnetic fields on the ductility and strength of materials. Voronezh, 2003, P. 232–233. Download (132 KB)
3. Vatutin E.I., Chevychelov S.Yu., Rodionov A.A., Ignatenko N.M. Modelling of processes of generation of elastic waves by an alternating magnetic field in magnetically ordered systems (in Russian) // Youth and XXI Century. Kursk, 2003. Part 3. P. 183–185. Download (235 KB)
4. Rodionov A.A., Ignatenko N.M., Vatutin E.I., Chevychelov S.Yu. Optimization of parameters of magnetostrictive transducer based on magnetically ordered systems (in Russian) // Materials and reinforcement technology – 2003. Kursk, 2003. Vol. 1. P. 89–93. Download (230 KB)
5. Vatutin E.I., Chevychelov S.Yu., Ignatenko N.M. Program for calculating the amplitude of the acoustic signal generated by the alternating magnetic field in magnetically ordered composites with solid and liquid matrices (in Russian) // Certificate of official registration of the computer software № 2008611513 from 25.03.08.

MULTISYSTEMS DESIGN
$\150dpi J\left( Sep_{F_k} \left( A_l^0 \right) \right) = \frac{K_H}{\omega_{max} }H + \frac{K_X}{\left| X \left( A_l^0 \right) \right|} \left( \sum_{i=1}^H \left| X \left( A_i \right) \right| - \left| X \left( A_l^0 \right) \right| \right) + \frac{K_Y}{\left| Y \left( A_l^0 \right) \right|} \left( \sum_{i=1}^H \left| Y \left( A_i \right) \right| - \left| Y \left( A_l^0 \right) \right| \right) +$
$\300dpi J\left( Sep_{F_k} \left( A_l^0 \right) \right) = \frac{K_H}{\omega_{max} }H + )\frac{K_X}{\left| X \left( A_l^0 \right) \right|} \left( \sum_{i=1}^H \left| X \left( A_i \right) \right| - \left| X \left( A_l^0 \right) \right| \right) + \frac{K_Y}{\left| Y \left( A_l^0 \right) \right|} \left( \sum_{i=1}^H \left| Y \left( A_i \right) \right| - \left| Y \left( A_l^0 \right) \right| \right) + \frac{K_{\delta}}{\delta \left( A_l^0 \right) } \delta \left( Sep_{F_k} \left( A_l^0 \right) \right) + \frac{K_{\alpha}}{\omega_{max} \left( \omega_{max} - 1 \right)} \sum_{i=1}^H \sum_{j=1, j \neq i}^H \alpha \left( A_i, A_j \right)$
1. Finding of the Base Section at the Problem of Getting Separations of Parallel Algorithms (in Russian) / Vatutin E.I., Zotov I.V.; Kursk State Technical University. Kursk, 2003. 30 p. Deposited by VINITI 24.11.2003. № 2036-B2003. Download (380 KB)
2. Vatutin E.I., Zotov I.V., Titov V.S. Building of the Set of Sections in the Problem of Optimal Separation of Parallel Logic Control Algorithms (in Russian) // Proceedings of Tula State University. Computer Sciences. Information Technologies. Control Systems. Vol. 1. Issue 2. 2003. P. 70–77. Download (274 KB)
3. Vatutin E.I., Zotov I.V. Building the Blocks of Separation in the Problem of Decomposition of Parallel Logic Control Algorithms (in Russian) // Materials and strengthening technologies – 2003. Kursk, 2003. Vol. 2. P. 38–42. Download (206 KB)
4. Vatutin E.I., Zotov I.V. Building the Matrix of Relations in the Problem of Getting Separations of Parallel Logic Control Algorithms (in Russian) // Proceedings of Kursk State Technical University. № 2. 2004. P. 85–89. Download (223 KB)
5. Vatutin E.I., Zotov I.V. Identification and Breaking of Sequential Loops in the Problem of Suboptimal Separation of Parallel Logic Control Algorithms (in Russian) // Proceedings of Tula State University. Computer Sciences. Information Technologies. Control Systems. Vol. 1. Issue 3. 2004. P. 51–55. Download (137 KB)
6. Vatutin E.I. Uniting Linear Ways at the Problem of Getting Suboptimal Separations of Parallel Logic Control Algorithms (in Russian) // Youth and XXI century. Part 1. 2004. P. 22–23. Download (163 KB)
7. Vatutin E.I., Zotov I.V. Method for Getting Suboptimal Separations of Parallel Logic Control Algorithms (in Russian) // Parallel Computing and Control Problems (PACO’04). Moscow: Institute of Control Problems of RAS, 2004. P. 884–917. Download (609 KB)
8. Vatutin E.I., Zotov I.V. Parallel-sequential Method for Getting Separations of Parallel Logic Control Algorithms (in Russian) // Certificate of official registration of the computer software № 2005613091 from 28.11.05.
9. Vatutin E.I., Zotov I.V. Program System for Getting Separations of Parallel Control Algorithms (in Russian) // Systems Identification and Control Problems (SICPRO’06). Moscow: Institute of Control Problems of RAS, 2006. P. 2239–2250. Download (417 KB)
10. Vatutin E.I. Constructing Random Sample Parallel Logic Control Algorithms // 11^th International Student Olympiad on Automatic Control (Baltic Olympiad, BOAC’06). Saint-Petersburg, 2006. P. 162–166. Download (eng) (129 KB), Download (rus) (238 KB)
11. Vatutin E.I., Abdel-Jalil J.N., Najajra M.H., Zotov I.V. Comparison of Methods for Getting Separation of Parallel Logic Control Algorithms // Information and Telecommunication Technologies in Intelligent Systems (ITT IS’06). Katania, Italy, 2006. PP. 92–94. Download (141 KB)
12. Vatutin E.I. The problem of estimation the intensity of the interblock interaction in the problem of finding the suboptimal separations of parallel control algorithms (in Russian) // Education, science, production. Belgorod, 2006. Download (202 KB), Презентация (390 KB)
13. Vatutin E.I. Assessment of the quality of separations of parallel control algorithms to sequential subalgorithms using the weighting function (in Russian) // Intellectual and Informational Systems (Intellect – 2005). Tula State University, 2005. P. 29–30. Download (124 KB)
14. Vatutin E.I., Zotov I.V. Visual environment for getting separations of parallel logic control algorithms (in Russian) // Certificate of official registration of the computer software № 2007613222 from 30.07.07.
15. Vatutin E.I., Volobuev S.V., Zotov I.V. A Comprehensive Comparative Evaluation of Methods for Getting Separations During Logic Multicontrollers Design (in Russian) // Systems Identification and Control Problems (SICPRO’08). Moscow: Institute of Control Problems of RAS, 2008. P. 1917–1940. Download (651 KB)
16. Vatutin E.I. Interesting properties of R-expressions in the problem of getting separations of parallel control algorithms (in Russian) // Youth and XXI Century. Kursk, 2008. Part 1. P. 30–31. Download (121 KB)
17. Vatutin E.I. Determining the parallelism degree of algorithm using matrix of relations (in Russian) // Modern instrumentation systems, information technologies and innovations. Part 2. Kursk, 2006. P. 135–139. Download (180 KB)
18. Vatutin E.I., Zotov I.V. Improving the quality of separations in the problem of synthesis of logic multicontrollers using parallel-sequential method (in Russian) // Prospects of Development of Weapon Control Systems. Moscow: Bedretdinov and Ko, 2007. P. 84–92. Download (292 KB)
19. Vatutin E.I. Parallel Logic Control Algorithm Separation Quality Analysis in the Synthesis of Logic Multicontrollers // 12^th International Student Olympiad on Automatic Control (Baltic Olympiad, BOAC'08). Saint-Petersburg, 2008. PP. 95-99. Download (eng) (187 KB), Download (rus) (289 KB)
20. Vatutin E.I., Volobuev S.V., Zotov I.V. A comprehensive comparative evaluation of methods for getting separations during logic multicontrollers design with technological constraints (in Russian) // Parallel Computing and Control Problems (PACO’08). Moscow: Institute of Control Problems of RAS, 2008. P. 643–685. Download (4,62 MБ)
21. Vatutin E.I. Determining the parallelism degree of graph-scheme of parallel algorithm (in Russian) // Intellectual and Informational Systems (Intellect – 2009). Tula State University, 2009. P. 24–26. Download (174 KB)
22. Vatutin E.I., Zotov I.V., Titov V.S. Identifing isomorphic inclusions of R-expressions during getting set of sections in the construction of sections of parallel logic control algorithms (in Russian) // Information-measuring and control systems. № 11, Vol. 7. Moscow: Radiotechnics, 2009. P. 49–56. Download (340 KB)
23. Vatutin E.I., Zotov I.V., Titov V.S. et al. Combinatorial-logic problems of getting separations of parallel logic control algorithms during logic multicontrollers design (in Russian) / Kursk: Kursk State Technical University, 2010. 200 p. ISBN 978-5-7681-0523-5.
24. Vatutin E.I. Logic multicontrollers design. Getting separations of parallel graph-schemes of algorithms (in Russian). Saarbrucken: Lambert Academic Publishing, 2011. 292 p. ISBN 978-3-8433-1728-3.
25. Vatutin E.I., Titov V.S. Comparison of methods for getting separations of parallel logic control algorithms using two-dimension diagrams (in Russian) // Recognition – 2012. Kursk: Southwest State University, 2012. P. 138–140. Download (340 KB) Video
26. Vatutin E.I., Titov V.S. Comparison of methods for the getting separations of the graph-schemes of parallel algorithms using two-dimensional diagrams (in Russian) // Proceedings of Southwest State University. № 3 (42), 2012. P. 66–74. Download (327 KB)
27. Vatutin E.I., Titov V.S. Using distributed volunteer computing systems for analysis of quality of separations of parallel logic control algorithms (in Russian) // Parallel Computing and Control Problems (PACO’12). Moscow: Institute of Control Problems of RAS, 2012. P. 37–54. Download (2,25 MB)
28. Vatutin E.I. Analysis of the effectiveness and program optimization of methods for getting separations of parallel logic control algorithms in PAE environment (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. № 2. Part 1. P. 191–195. Download (254 KB)
29. Vatutin E.I. Analysis of the bottlenecks of program implementation of parallel-sequential method for getting separations of parallel logic control algorithms (in Russian) // Recognition – 2013. Kursk: Southwest State University, 2013. P. 235–237. Download (188 KB)
30. Vatutin E.I. Library of Functions for Getting Separations Using S.I. Baranov Method with Greedy Consecutive Forming of Blocks (in Russian) // Certificate of official registration of the computer software № 2010612902 from 28.04.10.
31. Vatutin E.I., Valyaev S.Yu. Computing unit for getting separations of parallel logic control algorithms using volunteer computing (in Russian) // Certificate of official registration of the computer software № 2013618013 from 28.08.13.
32. Vatutin E.I., Titov V.S. Library of functions for getting separations with using adjacent greedy strategy and consecutive forming of blocks (in Russian) // Certificate of official registration of the computer software № 2013619395 from 03.10.13.
33. Vatutin E.I., Leonov M.E. Using adjacent neighborhood in the greedy consecutive forming of blocks of separations of graph-schemes of parallel algorithms (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. Vol. 56. № 6. P. 30–35. Download (468 KB)
34. Vatutin E.I., Titov V.S. Algorithmic optimization of program implementation of parallel-sequential method for getting separations of parallel logic control algorithms (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. Vol. 56. № 6. P. 23–29. Download (405 KB)
35. Vatutin E.I., Titov V.S. Structural-parametric optimization of logic control systems using volunteer computing (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. № 2. Part 1. 2012. P. 12–17. Download (249 KB)
36. Bobyntsev D.O., Vatutin E.I., Titov V.S. Estimation of the performance of matrix multiprocessor using parallel algorithm for solving the gravitational N-body problem (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. 2013. № 4. P. 20–28. Download (459 KB)
37. Vatutin E.I. Comparison of heuristic methods for getting separations of parallel logic control algorithms using volunteer computing at the BOINC platform (in Russian) // BOINC:FAST'2013. Video
38. Vatutin E.I., Titov V.S. Voluntary distributed computing for solving discrete combinatorial optimization problems using Gerasim@home project // Distributed computing and grid-technologies in science and education: book of abstracts of the 6th international conference. Dubna: JINR, 2014. PP. 60–61. ISBN 978-5-9530-0387-2. Презентация (1,9 MB)
39. Vatutin E.I., Mosin S.A., Titov V.S. Using Hungarian algorithm during inclusions tables analysis within the parallel-sequential approach during getting separations (in Russian) // Proceedings of Southwest State University. № 1 (52). 2014. P. 8–13. Download (261 KB)
40. Vatutin E.I., Kolyasnikov D.V., Martynov I.A., Titov V.S. Random search method at the problem of getting separations of parallel graph-schemes of algorithms (in Russian) // Multicore processors, parallel programming, FPGA, signal processing systems. Barnaul: Altay State University, 2014. P. 115–125. Download (319 KB)
41. Vatutin E.I., Kolyasnikov D.V., Titov V.S. Analysis of results of using random search method at the problem of getting separations of parallel graph-schemes of algorithms (in Russian) // Proceedings of South State University. Technical sciences. 2014. № 12 (161). P. 102–110. Download (256 KB)
42. Vatutin E.I., Titov V.S. Analysis of the areas of qualitative superiority of the sequential heuristic methods for getting separation during logic multicontrollers design (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. 2015. Vol. 58. № 2. P. 115-122. DOI: 10.17586/0021-3454-2015-58-2-115-122. Download (563 KB)
43. Vatutin E.I. Finding loops during processing graph-schemes of parallel algorithms using strongly connected components (in Russian) // Recognition – 2015. Kursk, 2015. P. 83–85. Download (195 KB) Video
44. Titov V.S., Vatutin E.I., Valyaev S.Yu., Andreev A.L. Analysis of probabilities of getting suboptimal decisions using adjacent greedy strategy of getting separations (in Russian) // Recognition – 2015. Kursk, 2015. P. 363–365. Download (204 KB)
45. Vatutin E.I. Discrete combinatorial problems solving using volunteer computing (in Russian) // Recognition – 2015, plenary report. Video
46. Vatutin E.I., Titov V.S. Library of functions for getting separations of parallel graph-schemes of algorithms using random search method (in Russian) // Certificate of official registration of the computer software № 2015618917 from 20.08.15.
47. Vatutin E.I., Valyaev S.Yu., Titov V.S. Comparison of Sequential Methods for Getting Separations of Parallel Logic Control Algorithms Using Volunteer Computing // CEUR Workshop Proceedings. Proceedings of the Second International Conference BOINC-based High Performance Computing: Fundamental Research and Development (BOINC:FAST 2015). Vol. 1502. Technical University of Aachen, Germany, 2015. P. 37–51. urn:nbn:de:0074-1502-3. Download (760 KB)
48. Vatutin E.I., Valyaev S.Yu., Titov V.S. Quality analysis of block separations of graph-schemes of parallel control algorithms during logic control systems design using grid systems on volunteer basis // Distributed computing and grid-technologies in science and education (GRID’16): book of abstracts of the 7th international conference. Dubna: JINR, 2016. p. 116–117. Download (65 KB), Slides
49. Vatutin E.I., Valyaev S.Yu., Titov V.S. Analysis of results of random search method during getting separations of graph-schemes of parallel algorithms depending from size of a problem and power of constraints (in Russian) // Perspective information technologies. Samara: Samara scientific center of RAS, 2016. P. 481–486. Download (161 KB)
50. Vatutin E.I., Titov V.S. On the selection of optimal structure organization of logic multicontrollers // Information-measurement technics and technologies 2016. Tomsk: TSU, 2016. P. 596–607. Download (242 KB)
51. Vatutin E.I., Titov V.S. On the selection of optimal structure organization of logic multicontrollers // MATEC Web of Conferences. Proceedings of the VII Scientific Conference with International Participation “Information-Measuring Equipment and Technologies” (IME&T 2016). Vol. 79. 2016. pp. 01084. DOI: 10.1051/matecconf/201679010 Download
52. Vatutin E.I., Titov V.S. On the selection of optimal structure organization of logic multicontrollers (in Russian) // Telecommunications. 2017. № 3. pp. 2–12. Download (371 KB)
53. Vatutin E.I., Panishev V.S., Gvozdeva S.N. Program for getting separations of graph-schemes of parallel logic control algorithms using weighted random search method (in Russian) // Certificate of official registration of the computer software № 2018611362 from 01.02.2018.
54. Vatutin E.I., Panishev V.S., Gvozdeva S.N., Titov V.S. Weighted random search method in the problem of getting separations of parallel logic control algorithms during logic multiconltrollers design (in Russian) // Proceedings of Southwest State University. 2017. Vol. 21. No. 6 (75). pp. 6–21. DOI: 10.21869/2223-1560-2017-21-6-6-21. Download (638 KB)
55. Vatutin E.I., Titov V.S. Estimation of the Hardware Complexity of Logical Multicontrollers Depending on the Values of Technological Limitations and Methods for Getting Separations of Graph-schemes of Parallel Algorithms (in Russian) // Science and education in the development of industrial, social and economic spheres of Russian regions. Murom, 2022. pp. 312–313. Download (296 KB)
56. Vatutin E.I., Titov V.S. Theoretical aspects and technical hardware and software solutions for the synthesis of logic multicontrollers (in Russian). Kursk: University book, 2022. 484 p. ISBN 978-5-907555-04-4. DOI: 10.47581/2022/Vatutin.01.

Results of the computing experiments

HARDWARE ORIENTED ACCELERATORS AND COPROCESSORS DESIGN

1. Borzov D.B., Vatutin E.I., Zotov I.V., Titov V.S. To the problem of suboptimal separations of parallel algorithms (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. Issue 12. 2004. P. 34–39. Download (143 KB)
2. Vatutin E.I., Zotov I.V. Hardware model for determining the minimal number of blocks during getting separations of parallel logic control algorithms (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. 2008. Vol. 51, № 2. P. 39–43. Download (274 KB)
3. Vatutin E.I. Homogeneous environment of electronic model of the tree for hardware-oriented processing of R-expressions (in Russian) // Recognition – 2008. Part 1. Kursk, 2008. P. 90–92. Download (241 KB)
4. Vatutin E.I., Zotov I.V., Titov V.S. Using circuit generators and converters of binary sequences during combinarotial-logic accelerators design (in Russian) // Proceedings of Kursk State Technical University. 2008. № 4 (25). P. 32–39. Download (493 KB)
5. Vatutin E.I., Zotov I.V., Titov V.S. Algorithm and device for getting isomorphic inclusions of R-expressions during building set of sections of parallel logic control algorithms (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. 2009. Vol. 52, № 2. P. 37–45. Download (375 KB)
6. Vatutin E.I. Hardware-oriented implementation of subtree deleting operation during processing of R-expressions (in Russian) // Recognition – 2010. Kursk, 2010. P. 162–164. Download (202 KB)
7. Vatutin E.I., Zotov I.V., Titov V.S., Al-Ashval M.M. Hardware-oriented implementation of subtree inserting operation processing of R-expressions (in Russian) // Proceedings of the Higher Educational Institutions. Instrument Making. 2010. Vol. 53, № 9. P. 63–71. Download (257 КB)
8. Vatutin E.I., Zotov I.V., Titov V.S. Hardware-oriented accelerator for fast transformations of constructive subsets of vertices of parallel algorithms (in Russian) // Parallel computing and Control Problems (PACO’10). Moscow: Institute of Control Problems of RAS, 2010. P. 1301–1366. Download (1,82 MB)
9. Martynov I.A., Vatutin E.I., Titov V.S. Hardware oriented classification of binary relations of graph-schemes of parallel algorithms // Eighth World Conference on Intelligent Systems for Industrial Automation (WCIS – 2014). Tashkent, 2014. PP. 70–73. Download (184 KB)
10. Martynov I.A., Vatutin E.I. Measuring of the real bandwidth of PCI Express bus using videocards with CUDA technology support as peripheral devices (in Russian) // Recognition – 2015. Kursk, 2015. P. 242–244. Download (229 KB)
11. Martynov I.A., Vatutin E.I., Titov V.S. Hardware-oriented implementation of transitive closure of binary relations (in Russian) // Recognition – 2015. Kursk, 2015. P. 244–247. Download (226 KB)
12. Najajra M.H., Martynov I.A., Vatutin E.I. Circuitry implementation of binary vectors multiplication operation during classification of binary relations of parallel graph-schemes of algorithms (in Russian) // Recognition – 2015. Kursk, 2015. P. 275–277. Download (238 KB)
13. Gvozdeva S.N., Vatutin E.I. Hardware complexity estimation for square binary matrix of order NxN multiplication device (in Russian) // Recognition — 2019. Kursk: SWSU, 2019. pp. 66–69. Download (216 KB)
14. Gvozdeva S.N., Vatutin E.I., Titov V.S. Speed evaluation of systolic device for multiplication of binary matrices (in Russian) // Telecommunications. Vol. 3. 2020. pp. 2–10. Download (475 KB)
15. Gvozdeva S.N., Vatutin E.I. Estimating the hardware complexity of a device for squaring a binary matrix (in Russian) // Medical-Ecological and Information Technologies - 2020. Part 2. Kursk, 2020. pp. 62-66. Download (286 KB)
16. Vatutin E.I., Gvozdeva S.N., Titov V.S. Mathematical model and hardware-oriented algorithm of a computing device for binary matrices processing (in Russian) // Recognition — 2021. Kursk, 2021. Video

Patents

Patent Russia Federation № 2336556, G06F9/28, G06F15/173, G06F1/10. Microcontroller network (in Russian) / Volobuev S.V., Zotov I.V., Krikunov O.V., Najajra M.H., Vatutin E.I. from 20.10.2008.

Patent Russia Federation № 2359320, G06F15/163. Module for messaging (in Russian) / Zotov I.V., Abdel-Jalil J.N., Vatutin E.I., Volobuev S.V., Krikunov O.V., Najajra M.H. from 20.06.2009.

Patent Russia Federation № 2360283, G06F15/163, H03K17/00. Switching module with parallel-pipelined processing and broadcasting of messages (in Russian) / Krikunov O.V., Najajra M.H., Zotov I.V., Borzov D.B., Vatutin E.I., Volobuev S.V. from 27.06.2009.

Patent Russia Federation № 2371766, G06N7/00, G06F17/00. Device for the study of graphs (in Russian) / Vatutin E.I., Zotov I.V. from 27.10.2009.

Utility patent Russia Federation № 127872. Subscriber entering the heating system of the building (in Russian) / Zarubin A.N., Fedorov S.S., Vatutin E.I., Kobelev N.S. from 06.12.2012.

Utility patent Russia Federation № 157948. Device for the matrices multiplication (in Russian) / Vatutin E.I., Martynov I.A., Titov V.S. from 08.07.2015.
Utility patent Russia Federation № 193927. Device for the binary matrices multiplication (in Russian) / Gvozdeva S.N., Vatutin E.I., Pshenichnikh A.O., Titov V.S. from 21.11.2019.
Patent Russia Federation № 2744239. Binary matrix squaring device (in Russian) / Gvozdeva S.N., Vatutin E.I., Titov V.S. from 04.03.2021.

PROGRAM OPTIMIZATION OF SOFTWARE
$\150dpi Z_1 = X \cap Y, Z_2 = X \cup Y, Z_3 = X \setminus Y, Z_4 = \overline{X}$

$\150dpi H_x = \begin{pmatrix} h_x^{11} & h_x^{12} & h_x^{13} \\ h_x^{21} & h_x^{22} & h_x^{23} \\ h_x^{31} & h_x^{32} & h_x^{33} \end{pmatrix} = \begin{pmatrix} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{pmatrix}$
$\150dpi H_y = \begin{pmatrix} h_y^{11} & h_y^{12} & h_y^{13} \\ h_y^{21} & h_y^{22} & h_y^{23} \\ h_y^{31} & h_y^{32} & h_y^{33} \end{pmatrix} = \begin{pmatrix} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{pmatrix}$
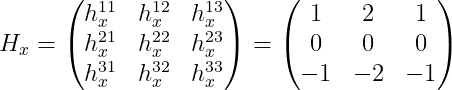
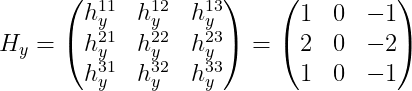
$\150dpi d_i(x, y) = f(x, y) \cdot H_i = \sum_{j=1}^3 \sum_{k=1}^3 f(x+j-2, y+k-2) \cdot h_i^{jk}, i \in \{x, y \}$
$\150dpi g(x, y) = \sqrt{d_x^2(x, y) + d_y^2(x, y)}$

$\150dpi p = \frac {a + b + c} {2}, S = \sqrt {p(p-a)(p-b)(p-c)}$

$\150dpi \sin x = x - \frac {x^3}{3!} + \frac {x^5}{5!} - ... = \sum_{i=1}^{\infty} (-1)^{i+1} \frac{x^{2i-1} }{ (2i-1)! }$

$\150dpi r_{ij} = \sqrt{\left( \Delta x_{ij} \right)^2 + \left( \Delta y_{ij} \right)^2}$
$\150dpi a_i^{(x)} = G \sum_{j=1, i \ne j}^N \frac{m_j}{r_{ij}^3} \Delta x_{ij}$
$\150dpi a_i^{(y)} = G \sum_{j=1, i \ne j}^N \frac{m_j}{r_{ij}^3} \Delta y_{ij}$
$\150dpi \vec{v}_i^{(t)} = \vec{v}_i^{(t-1)} + \vec{a}_i \Delta t$
$\150dpi \vec{X}_i^{(t)} = \vec{X}_i^{(t-1)} + \vec{v}_i \Delta t$
$\150dpi \vec{v}^{*} = \frac{m_i v_i + m_j v_j}{m_i + m_j}$

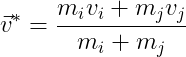
1. Vatutin E.I. Optimization of sets processing (in Russian) // Medical and ecological imformation technologies 2005. Kursk, 2005. P. 145–147. Download (181 KB)
2. Vatutin E.I., Miroshnichenko S.Yu., Titov V.S. Program optimization of Sobel operator using SIMD-extensions of x86 processors family (in Russian) // Telecommunications. 2006. № 6. P. 12–16. Download (339 KB)
3. Vatutin E.I. SIMD-optimizing of mathematical calculations on the example of the problem of calculating the area of a triangle (in Russian) // Youth and XXI century. Part 1. Kursk, 2006. P. 10–11. Download (123 KB), Slides (213 KB)
4. Vatutin E.I. Library of classes for sets processing with SIMD-optimization (in Russian) // Certificate of official registration of the computer software № 2007614221 from 03.08.07.
5. Vatutin E.I. SIMD-optimization of sine function calculation using Taylor series (in Russian) // Certificate of official registration of the computer software № 2007614222 от 03.08.07.
6. Vatutin E.I., Miroshnichenko S.Yu., Degtyarev S.V., Titov V.S. SIMD-optimized version of Sobel operator (in Russian) // Certificate of official registration of the computer software № 2008611514 from 25.03.08.
7. Kobzar E.Yu., Vatutin E.I. Methodology of precise measuring the performance of fragments of program code in multitasking operating systems (in Russian) // Recognition – 2008. Part 2. Kursk, 2008. P. 180–181. Download (186 KB)
8. Vatutin E.I., Titov V.S. Features of realization the Hyper-threading technology in the Intel Pentium 4 processors at the different types of code (in Russian) // Proceesings of Kursk State Technical University. Kursk, 2008. № 2 (23). P. 62–65. Download (299 KB)
9. Vatutin E.I. SIMD-optimization of trigonometric functions at the example of sine function calculating (in Russian) // Youth and XXI century. Part 1. Kursk, 2008. P. 29–30. Download (132 KB)
10. Vatutin E.I., Martynov I.A., Titov V.S. The CPU real performance estimation for matrices multiplication problem using single-threaded software implementation (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. 2013. № 4. С. 11–20. Download (279 KB)
11. Vatutin E.I. Program for numerical solution of the N-body problem with SIMD-optimization (in Russian) // Certificate of official registration of the computer software № 2013619781 from 15.10.13.
12. Vatutin E.I., Martynov I.A., Titov V.S. The GPU real performance estimation for matrices multiplication problem using CUDA (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. 2014. № 2. P. 8–17. Download (318 KB)
13. Vatutin E.I., Martynov I.A., Titov V.S. The CPU and GPU with CUDA support real performance estimation for matrices multiplication problem (in Russian) // CUDA almanac (may 2015). 2015. P. 9–10. Download (1,5 MB)
14. Vatutin E.I., Titov V.S. The CPU real performance estimation for matrices multiplication problem using single-threaded program implementation with SSE extension support (part 1) (in Russian) // Proceedings of Southwest State University. 2015. Vol. 1. № 4 (61). P. 26–35. Download (343 KB)
15. Vatutin E.I., Titov V.S. The CPU real performance estimation for matrices multiplication problem using single-threaded program implementation with SSE extension support (part 2) (in Russian) // Proceedings of Southwest State University. 2015. Vol. 1. № 5 (62). P. 8–16. Download (335 KB)
16. Zatolokin Yu.A., Vatutin E.I., Titov V.S. The GPU real performance estimating for matrices multiplication using OpenCL (in Russian) // Recognition — 2017. Kursk: SWSU, 2017. P. 164–167. Download (252 KB)
17. Popov D.V., Nadjadjra M.H., Vatutin E.I. The time costs analysis of heuristic methods using CUDA technology in the shortest path problem (in Russian) // Recognition — 2017. Kursk: SWSU, 2017. P. 285–287. Download (217 KB)
18. Popov D.V., Vatutin E.I. Analysis of the effectiveness of GPGPU technology during implementing heuristic algorithms for graph problems (in Russian) // Visual analytics 2017. Kemerovo: Kuzbassvuzizdat, 2017. pp. 37–39. Download (225 KB)
19. Zatolokin Y.A., Vatutin E.I., Titov V.S. Algorithmic optimization of software implementation of algorithms for multiplying dense real matrices on graphics processors with OpenCL technology support (in Russian) // Proceedings of the Southwest State University, 2017, vol. 21, no. 5(74), pp. 6-15. DOI: 10.21869/2223-1560-2017-21-5-06-15. Download (350 KB)
17. Gvozdeva S.N., Vatutin E.I. Estimating of the probability of early interruption of the process of multiplication of binary matrices from their size and density (in Russian) // Recognition — 2021. Kursk, 2021. pp. 87–90. Download (548 KB)

SCHEDULING
$\150dpi f $ \Theta $ = \frac {K^{(t)}_w t_w (\Theta)} {2Dw^{(t)}_{\max}T} + \frac {K^{(s)}_w s_w (\Theta)} {2Dw^{(s)}_{\max}S} + \frac {K^{(t)}_{wt} t_{wt} (\Theta)} {2Dp^{(t)}_{\max}T} + \frac {K^{(s)}_{wt} s_{wt} (\Theta)} {2Dp^{(s)}_{\max}S} +$
$\150dpi + \frac {K^{(a)}_{wt} a_{wt} (\Theta)} {2DPA} + \frac {K^{(w)}_a w_a (\Theta)} {\left | \Theta \right|} + \frac {K^{(t)}_g t_g (\Theta)} {2DT} +$
$\150dpi + \frac {K^{(t)}_{p_{\min}} t_{p_{\min}} (\Theta)} {2DT} + \frac {K^{(t)}_{p_{\max}} t_{p_{\max}} (\Theta)} {2DT} + \frac {K^{(t)}_{l_{\max}} t_{l_{\max}} (\Theta)} {2DT} +$
$\150dpi + \frac {K^{(s)}_{p_{\min}} s_{p_{\min}} (\Theta)} {2DS} + \frac {K^{(s)}_{p_{\max}} s_{p_{\max}} (\Theta)} {2DS} + \frac {K^{(s)}_{l_{\max}} s_{l_{\max}} (\Theta)} {2DS} +$
$\150dpi + \frac {K^{(s)}_{ed} s_{ed} } {2DS} + \frac {K^{(t)}_m t_m } {2DT \cdot $ \max m_{ij} + 1 $} + \frac {K^{(s)}_m s_m } {2DS \cdot $ \max m_{ij} + 1 $}$

Vatutin V.I., Vatutin E.I., Romanchenko A.S. Automation of scheduling in KurskSTU (in Russian) // Modern problems of higher professional education. Kursk, 2010. Part 1. P. 28–30.
Vatutin E.I., Vatutin V.I., Shirabakina T.A. Network data model at the problem of automation of scheduling in KurskSTU (in Russian) // Recognition – 2010. Kursk, 2010. P. 218–220. Download (182 KB)
Vatutin V.I., Vatutin E.I. The software package for the automation of the training department of the university (in Russian) // Intellectual and information systems. Tula, 2011. P. 20–21.
Vatutin E.I., Vatutin V.I., Romanchenko A.S. Assessment of the quality of high school schedules using the weighting function (in Russian) // Recognition – 2012. Kursk, 2012. P. 136–138. Download (180 KB)
Vatutin E.I., Bobyntsev D.O., Romanchenko A.S. Program for greedy construction of the schedule of studies of the university (in Russian) // Certificate of official registration of the computer software № 2013618554 from 11.09.13.
Vatutin E.I., Romanchenko A.S., Titov V.S. Investigation of influence of the pairs order consideration to sсhedule quality within greedy approach (in Russian) // Proceedings of Southwest State University. 2013. № 1 (46). P. 58–64. ISSN 2223-1560 Download (230 KB)
Vatutin E.I., Bobyntsev D.O., Romanchenko A.S. Investigation of influence of the partial pairs ordering and pair vicinity improvement to schedule quality within greedy approach (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. 2014. № 1. P. 8–16. Download (251 KB)
Vatutin E.I., Bobyntsev D.O., Romanchenko A.S. The method of constructing a greedy university schedule with a random order of consideration of the study groups and the improvement of the neighborhood of the current pair (in Russian) // Certificate of official registration of the computer software № 2013619101 from 25.09.13.

EDUCATION

Vatutin E.I. The automated software system for testing students' knowledge in the discipline «Programming with Delphi» (in Russian) // Certificate of official registration of the computer software № 2007610411 from 24.01.07.
Vatutin E.I., Симонова Ж.Г. The automated software system for testing students' knowledge of English «Modal verbs» (in Russian) // Certificate of official registration of the computer software № 2007612055 from 22.05.07.
Vatutin E.I. Comparison of algorithms for sorting arrays (in Russian) // Youth and XXI century. Part 1. Kursk, 2007. P. 19–20. Презентация (1,0 MB)
Zotov I.V., Vatutin E.I., Borzov D.B. Procedure-oriented programming with С++ (in Russian). Kursk, 2008. 211 p. ISBN 978-5-7681-0356-9.
Vatutin E.I. et al. Procedure-modular programming with Delphi (in Russian). Moscow: Argamac-Media, 2014. 352 p. ISBN 978-5-00024-020-5.

VOLUNTEER COMPUTING (BOINC)

Andreev A.L., Manzyuk M.M., Vatutin E.I. The whole world is like a supercomputer (in Russian) // Troitsk variant — science. № 16 (110) from 14.08.2012. P. 7. Download (4,2 MB)
Posypkin M., Vatutin E., Kurochkin I., Khrapov N., Ivashko E., Zaikin O., Andreev A., Afanasiev A. The activity of Russian chapter of international desktop grid federation // Distributed computing and grid-technologies in science and education: book of abstracts of the 6th international conference. Dubna: JINR, 2014. p. 46.
Kurochkin I.I., Posypkin M.A., Andreev A.A., Vatutin E.I., Zaikin O.S., Putilina E.V., Manzuk M.O. The activity of Russian chapter of international desktop grid federation // Distributed computing and grid-technologies in science and education (GRID’16): book of abstracts of the 7th international conference. Dubna: JINR, 2016. p. 36.

GRAPH THEORY, COMBINATORIAL OPTIMIZATION

Heuristic methods at the problem of getting single shortest path in graph

Dremov E.N., Vatutin E.I. Comparison the quality of decisions by different methods at the shortest path problem (in Russian) // Recognition – 2013. Kursk, 2013. P. 249–251. Download (199 KB)
Vatutin E.I., Martynov I.A., Titov V.S. Method of Workaround deadlocks for solving discrete combinatorial optimization problems with constraints (in Russian) // Perspective information technologies. Samara: Samara scientific center of RAS. P. 313–317. Download (136 KB)
Vatutin E.I., Dremov E.N., Martynov I.A., Titov V.S. Weighted random search mehod for discrete combinatorial problems solving (in Russian) // Proceedings of Volgograd State University. Series: Electronics, measurement equipment, radio engineering and communications. № 10 (137). Iss. 9. 2014. P. 59–64. Download (304 KB)
Vatutin E.I., Valyaev S.Yu., Dremov E.N., Martynov I.A., Titov V.S. Computing unit for testing combinatorial optimization algorithms at the shortest path problem using volunteer computing (in Russian) // Certificate of official registration of the computer software № 2014619797 from 22.09.14.
Vatutin E.I., Titov V.S. Analysis of results of using ant colony optimization method at the shortest path problem with constraints (in Russian) // Proceedings of South State University. Technical sciences. 2014. № 12 (161). P. 111–120. Download (292 KB)
Vatutin E.I., Martynov I.A., Titov V.S. Analysis of results of depth first search with fixed depth method at the shortest path problem (in Russian) // Multicore processors, parallel programming, FPGA, signal processing systems. Barnaul: Altay State University, 2015. P. 120–128. Download (374 KB)
Vatutin E.I., Titov V.S. Parametric optimization of simulated annealing algorithm at the shortest path problem (in Russian) // Proceedings of Cherepovets State University. № 6 (67). 2015. P. 13–16. Download (276 KB)
Vatutin E.I., Titov V.S. An approach to the use of an ant colony algorithm during discrete combinatorial optimization problems solving (in Russian) // Intellectual and information systems. Tula, 2015. P. 8–13. Download (219 KB)
Vatutin E.I., Titov V.S. The features of use genetic algorithm in the problem of finding the shortest path in the graph with graph density constraint (in Russian) // Multicore processors, parallel programming, FPGA, signal processing systems. Barnaul: Altay State University, 2016. P. 152–159. Download (374 KB)
Vatutin E.I., Valyaev S.Yu., Titov V.S. Using volunteer computing for comparison of quality of decisions of heuristic methods in the problem of getting shortest path in the graph with graph density constraint // Distributed computing and grid-technologies in science and education (GRID’16): book of abstracts of the 7th international conference. Dubna: JINR, 2016. p. 117–119. Download (76 KB), Slides
Vatutin E.I., Titov V.S. Convergence rate analysis of quality of decisions of heuristic methods at the shortest path problem (in Russian) // Information-measuring and diagnosing control systems (Diagnostics – 2016). Kursk: SWSU, 2016. P. 19–25. Download (457 КБ)
Vatutin E.I., Titov V.S. Time costs analysis during getting decisions of heuristic methods at the shortest path problem (in Russian) // Information-measuring and diagnosing control systems (Diagnostics – 2016). Kursk: SWSU, 2016. P. 26–33. Download (903 КБ)
Vatutin E.I., Titov V.S. Features of meta-optimization of the bee colony method in the shortest path problem with constraints on the graph density (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. № 2 (19). 2016. P. 52–65. Download (797 КБ)
Vatutin E.I., Titov V.S. Investigation of the features of particle swarm optimization method in discrete optimization problems (in Russian) // Proceedings of the 10th multiconference on control problems. Vol. 3. Rostov-on-Don, Taganrog, 2017. P. 20–22. Download (163 KB)
Vatutin E.I. Comparison of Decisions Quality of Heuristic Methods with Sequential Formation of the Decision in the Graph Shortest Path Problem // CEUR Workshop Proceedings. Proceedings of the Third International Conference BOINC-based High Performance Computing: Fundamental Research and Development (BOINC:FAST 2017). Vol. 1973. Technical University of Aachen, Germany, 2017. pp. 67–76. urn:nbn:de:0074-1973-0. Download (14,3 МБ)
Vatutin E.I. Comparison of Decisions Quality of Heuristic Methods with Limited Depth-First Search Techniques in the Graph Shortest Path Problem // Open Engineering. Vol. 7. Iss. 1. 2017. pp. 428–434. DOI: 10.1515/eng-2017-0041. Download
Vatutin E.I., Titov V.S. Investigation of features of particle swarm optimization method in graph shortest path problem with constraints (in Russian) // Herald of computer and information technologies. No. 5 (167). 2018. pp. 26–34. DOI: 0.14489/vkit.2018.05.pp.026–034. Download (832 KB)
Vatutin E.I., Panishchev V.S., Gvozdeva S.N., Titov V.S. Comparison of Decisions Quality of Heuristic Methods Based on Modifying Operations in the Graph Shortest Path Problem // IX International Conference on Optimization Methods and Applications "Optimization and Applications (OPTIMA-2018)", Book of Abstracts. Moscow, Petrovac, 2018. P. 171. Download (32 KB)
Vatutin E., Panishchev V., Gvozdeva S., Titov V. Comparison of Decisions Quality of Heuristic Methods Based on Modifying Operations in the Graph Shortest Path Problem // Problems of Information Technology. No. 1. 2020. pp. 3–15. DOI: 10.25045/jpit.v11.i1.01. Download (829 KB)

Heuristic methods at the problem of getting quasi-optimal coloring in graph

Kolyasnikov D.V., Vatutin E.I. An analysis of the degree of approximation to the optimum for chromatical number of graph with using heuristic methods (in Russian) // Recognition – 2013. Kursk, 2013. P. 253–255. Download (186 KB)
Pshenichnykh A.O., Vatutin E.I. Comparison of decisions quality of heuristic methods for graph chromatic number determining (in Russian) // Recognition — 2017. Kursk: SWSU, 2017. P. 287–289. Download (348 KB)
Pshenichnykh A.O., Vatutin E.I. An analysis of decisions quality for weighted random search method in the problem of heuristic estimation of graph chromatic number (in Russian) // Intellectual and Information Systems (Intellect – 2017). Tula, 2017. pp. 95–99. Download (596 KB)
Pshenichnykh A.O., Vatutin E.I., Titov V.S. The influence of the color of the first vertex for the greedy method for estimating the chromatic number of a graph (in Russian) // Recognition — 2019. Kursk: SWSU, 2019. pp. 144–146. Download (257 KB)
Pshenichnykh A.O., Vatutin E.I. The influence of the probability of choosing the minimum possible or random color for the greedy method for estimating the chromatic number of a graph (in Russian) // Prospective information technologies. Samara: Samara scientific center of RAS, 2019. pp. 348–351. Download (204 KB)
Pshenichnykh A.O., Gvozdeva S.N., Vatutin E.I. Investigation of the influence of the order of consideration of vertices during graphs coloring using greedy algorithm (in Russian) // High-performance computing systems and technologies. Vol. 3. No. 1. 2019. pp. 101–106. Download (401 KB)
Pshenichnykh A.O., Gvozdeva S.N., Panishchev V.S., Vatutin E.I. The influence of the probability of choosing the minimum possible or random color for the random search method for estimating the chromatic number of a graph (in Russian) // Intellectual and Information Systems (Intellect – 2019). Tula, 2019. pp. 59–63. Download (305 KB)
Pshenichnykh A.O., Vatutin E.I. The influence of the choice of the initial color on the quality of solutions for the weighted random search during graph coloring search (in Russian) // Advanced Information Technology. Samara, 2020. pp. 228–232. Download (238 KB)
Pshenichnykh A.O., Vatutin E.I. On the choice of an initial solution when searching for a suboptimal graph coloring using the random walk method (in Russian) // Medical-Ecological and Information Technologies - 2020. Part 2. Kursk, 2020. pp. 81-86. Download (749 КБ)
Pshenichnykh A.O., Vatutin E.I. On the stochastic initial filling of the pheromone matrix during the estimate of the chromatic number of the graph for the ant colony optimization method (in Russian) // Recognition — 2021. pp. 206–208. Download (413 KB)

Diagonal Latin squares
Random DLS generation
Vatutin E.I., Zhuravlev A.D., Zaikin O.S., Titov V.S. Features of using weighting heuristics in the problem of finging diagonal Latin squares (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. 2015. № 3 (16). pp. 18–30. Download (328 KB)
Vatutin E.I., Zhuravlev A.D., Zaikin O.S., Titov V.S. Using algorithmic features in the problem of generating diagonal Latin squares (in Russian) // Proceedings of Southwest State University. 2016. № 2 (65). P. 46–59. Download (353 KB)
Vatutin E.I., Titov V.S., Zaikin O.S., Zhuravlev A.D., Manzuk M.O., Kochemazov S.E. Program for getting diagonal Latin squares of selected order using heuristic methods (in Russian) // Certificate of official registration of the computer software № 2016662288 from 07.11.16.

Pseudotriples of MODLS
Zaikin O.S., Vatutin E.I., Zhuravlev A.D., Manzyuk M.O. Applying high-performance computing to searching for triples of partially orthogonal Latin squares of order 10 (in Russian) // Parallel computational technologies (PCT’2016). Chelyabinsk, 2016. pp. 155-166. Download (746 КБ)
Zaikin O.S., Vatutin E.I., Zhuravlev A.D., Manzyuk M.O. Applying High-Performance Computing to Searching for Triples of Partially Orthogonal Latin Squares of Order 10 (in Russian) // Bulletin of the South Ural State University. Series: Computational Mathematics and Software Engineering. 2016. Vol. 5, No. 3. P. 54–68. DOI: 10.14529/cmse160304. Download
Zaikin O.S., Vatutin E.I., Zhuravlev A.D., Manzyuk M.O. Applying high-performance computing to searching for triples of partially orthogonal Latin squares of order 10 // CEUR Workshop Proceedings. Proceedings of the 10th Annual International Scientific Conference on Parallel Computing Technologies "Parallel Computing Technologies" (PCT 2016). Vol. 1576. 2016. P. 155–166. urn:nbn:de:0074-1576-1. Download (746 KB)
Zaikin O., Zhuravlev A., Kochemazov S., Vatutin E. On the Construction of Triples of Diagonal Latin Squares of Order 10 // Electronic Notes in Discrete Mathematics. Vol. 54C. 2016. P. 307–312. DOI: 10.1016/j.endm.2016.09.053 Download (88 KB)
Malkov V.V., Vatutin E.I. Getting pseudotriples of diagonal Latin squares of order 10 using random search method (in Russian) // Intellectual information systems: trends, problems, prospects. Kursk: SWSU, 2022. pp. 113–116. Download (263 KB)

Enumeration of DLS
Vatutin E.I., Zaikin O.S., Zhuravlev A.D., Manzuk M.O., Kochemazov S.E., Titov V.S. Using grid systems for enumerating combinatorial objects on example of diagonal Latin squares // Distributed computing and grid-technologies in science and education (GRID’16): book of abstracts of the 7th international conference. Dubna: JINR, 2016. p. 114–115. Download (31 KB), Slides
Vatutin E.I., Zaikin O.S., Zhuravlev A.D., Manzuk M.O., Kochemazov S.E., Titov V.S. The effect of filling cells order to the rate of generation of diagonal Latin squares (in Russian) // Information-measuring and diagnosing control systems (Diagnostics – 2016). Kursk: SWSU, 2016. P. 33–39. Download (171 KB)
Vatutin E.I., Titov V.S., Zaikin O.S., Kochemazov S.E., Valyaev S.Yu., Zhuravlev A.D., Manzuk M.O. Using grid-systems for enumerating combinatorial objects on example of diagonal Latin squares of order 9 (in Russian) // Information technologies and mathematical modeling of systems 2016. M.: Center for Information Technology in the design of the RAS, 2016. P. 154–157. Download (186 KБ)
Zaikin O.S., Kochemazov S.E., Vatutin E.I., Titov V.S., Valyaev S.Yu., Zhuravlev A.S., Manzuk M.O. Enumeration of combinatorial objects on example of diagonal Latin squares using volunteer computing // National supercomputing forum (NSCF — 2016). Pereslavl-Zalessky, 2016. Slides (736 KB)
Vatutin E.I., Titov V.S., Zaikin O.S., Zhuravlev A.D., Manzuk M.O., Kochemazov S.E., Fedorov S.S. Program for recurrent enumerating of diagonal Latin squares of selected order using brute force approach and its modifications (in Russian) // Certificate of official registration of the computer software № 2016662287 from 07.11.16.
Vatutin E.I., Zaikin O.S., Zhuravlev A.D., Manzyuk M.O., Kochemazov S.E., Titov V.S. Using grid systems for enumerating combinatorial objects on example of diagonal Latin squares // CEUR Workshop proceedings. Selected Papers of the 7th International Conference Distributed Computing and Grid-technologies in Science and Education. 2017. Vol. 1787. pp. 486–490. urn:nbn:de:0074-1787-5. Download (193 KB)
Kochemazov S.E., Vatutin E.I., Zaikin O.S. Fast Algorithm for Enumerating Diagonal Latin Squares of Small Order // arXiv:1709.02599 [math.CO], 2017. 31 p.
Vatutin E.I., Kochemazov S.E., Zaikin O.S. Applying volunteer and parallel computing for enumerating diagonal Latin squares of order 9 // Proc. of The Eleventh International Conference on Parallel Computational Technologies, Vol. 753 of Communications in Computer and Information Science, Springer, 2017, pp. 114–129. DOI: 10.1007/978-3-319-67035-5_9. Download
Kochemazov S., Zaikin O., Vatutin E., Belyshev A. Enumerating Diagonal Latin Squares of Order Up to 9 // Journal of Integer Sequences. Vol. 23. Iss. 1. 2020. Article 20.1.2. Download (212 KB)
Shaldunov I.I., Vatutin E.I. Comparison of methods for filling diagonal Latin squares within an iterative implementation of the Brute Force method (in Russian) // Cloud and distributed computing systems in electronic control conference, within the National supercomputing forum (NSCF — 2022). Pereslavl-Zalessky, 2023. pp. 51–59. Download (227 KB)
Vatutin E.I., Belyshev A.D., Nikitina N.N., Manzuk M.O. Use of X-based diagonal fillings and ESODLS CMS schemes for enumeration of main classes of diagonal Latin squares (in Russian) // Telecommunications. 2023. No. 1. pp. 2–16. DOI: 10.31044/1684-2588-2023-0-1-2-16. Download (319 KB)

Isomorphism classes of DLS
Vatutin E., Belyshev A., Kochemazov S., Zaikin O., Nikitina N. Enumeration of isotopy classes of diagonal Latin squares of small order using volunteer computing // Supercomputing Days Russia 2018. M.: Moscow State University, 2018. pp. 933–942. Download (478 KB), Slides
Vatutin E., Belyshev A., Kochemazov S., Zaikin O., Nikitina N. Enumeration of isotopy classes of diagonal Latin squares of small order using volunteer computing // Communications in Computer and Information Science. Vol. 965. Springer, 2018. pp. 578–586. DOI: 10.1007/978-3-030-05807-4_49. Download

Reduction of the DLS/ODLS problems to the exact cover problem and solving it using DLX
Shutov I.V., Kochemazov S.E., Kurochkin I.I., Zaikin O.S., Vatutin E.I. Using GPU for searching pairs of orthogonal diagonal Latin squares of order 10 (in Russian) // Russian Supercomputing Days 2016. M.: MSU, 2016. P. 180–184. Download (731 KB)
Vatutin E.I. On polynomial reduction of problems based on diagonal Latin squares to the exact cover problem. And related results… // Recognition — 2019. Plenary report. Slides (1,9 MB)
Vatutin E.I., Belyshev A.D., Kochemazov S.E., Zaikin O.S., Nikitina N.N., Manzuk M.O. On polynomial reduction of problems based on diagonal Latin squares to the exact cover problem (in Russian) // Recognition — 2019. Kursk: SWSU, 2019. pp. 62–64. Download (203 KB)
Vatutin E., Nikitina N., Belyshev A., Manzyuk M. On polynomial reduction of problems based on diagonal Latin squares to the exact cover problem // CEUR Workshop Proceedings. Proceedings of the Second International Conference Information, Computation, and Control Systems for Distributed Environments (ICCS-DE 2020). Vol. 2638. Technical University of Aachen, Germany, 2020. pp. 289-297. urn:nbn:de:0074-2638-1. DOI: 10.47350/ICCS-DE.2020.26. Download (593 KB)
Albertyan A.M., Qurochkin I.I., Vatutin E.I. Optimizing the performance of a heterogeneous computing system when solving the problem of finding orthogonal diagonal Latin squares (in Russian) // Recognition — 2021. Kursk, 2021. Video

Search for ODLS with different types of orthogonality
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Citerra I.I. Estimation of the probability of finding orthogonal diagonal Latin squares among general diagonal Latin squares (in Russian) // Recognition – 2018. Kursk: SWSU, 2018. pp. 72–74. Download (242 KB)
Vatutin E.I., Belyshev A.D. About the number of self-orthogonal (SODLS) and doubly self-orthogonal diagonal Latin squares (DSODLS) of orders 1–10 (in Russian) // High-performance computing systems and technologies. Vol. 4. No. 1. 2020. pp. 58–63. Download (279 KB), Slides (13,6 MB)
Vatutin E., Belyshev A. Enumerating the Orthogonal Diagonal Latin Squares of Small Order for Different Types of Orthogonality // Communications in Computer and Information Science. Vol. 1331. Springer, 2020. pp. 586–597. Download
Vatutin E., Belyshev A., Nikitina N., Manzuk M. Evaluation of Efficiency of Using Simple Transformations When Searching for Orthogonal Diagonal Latin Squares of Order 10 // Communications in Computer and Information Science. Vol. 1304. Springer, 2020. pp. 127–146. DOI: 10.1007/978-3-030-66895-2_9. Download

Numerical characteristics of DLS
Vatutin E.I., Kochemazov S.E., Zaikin O.S. Estimating of combinatorial characteristics for diagonal Latin squares (in Russian) // Recognition — 2017. Kursk: SWSU, 2017. P. 98–100. Download (199 KB)
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Manzuk M.O., Titov V.S. Combinatorial characteristics estimating for pairs of orthogonal diagonal Latin squares (in Russian) // Multicore processors, parallel programming, FPGA, signal processing systems. Barnaul: Altay State University, 2017. pp. 104–111. Download (154 KB)
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Valyaev S.Yu. Enumerating the Transversals for Diagonal Latin Squares of Small Order // CEUR Workshop Proceedings. Proceedings of the Third International Conference BOINC-based High Performance Computing: Fundamental Research and Development (BOINC:FAST 2017). Vol. 1973. Technical University of Aachen, Germany, 2017. pp. 6–14. urn:nbn:de:0074-1973-0. Download (826 KB)
Vatutin E.I., Kochemazov S.E., Zaikin O.S. Algorithmic optimization of the program implementation of the procedure for obtaining a set of transversals procedure for Latin squares (in Russian) // Visual analytics 2017. Kemerovo: Kuzbassvuzizdat, 2017. pp. 44–49. Download (260 KB)
Vatutin E.I., Zaikin O.S., Kochemazov S.E., Valyaev S.Yu., Titov V.S. Estimating the Number of Transversals for Diagonal Latin Squares of Small Order (in Russian) // Telecommunications. 2018. No. 1. pp. 12-21. Download (346 KB)
Vatutin E.I., Zaikin O.S., Kochemazov S.E., Manzuk M.O. Program for getting transversals set for diagonal Latin squares and getting orthogonal squares using Brute Force approach (in Russian) // Certificate of official registration of the computer software № 2018610473 from 11.01.2018.
Vatutin E.I. Estimating the maximal size of main class for diagonal Latin squares of orders 9-15 (in Russian) // Medical-Ecological and Information Technologies – 2020. Part 2. Kursk, 2020. pp. 57–62. Download (263 KB)
Vatutin E.I. Numerical Sequences, Enumerative Combnatorics and Related Branches of Mathematics // Recognition — 2021. Plenary report. Slides (1,9 МБ) Video
Vatutin E.I. 2-transversals in pairs of orthogonal diagonal Latin squares (in Russian) // Recognition — 2021. pp. 77–79. Download (216 KB), Slides (1,6 MB)
Vatutin E.I., Nikitina N.N., Manzuk M.O., Kurochkin I.I., Albertyan A.M. About the number of transversals in diagonal Latin squares of even orders (in Russian) // National supercomputing forum (NSCF — 2023). Pereslavl-Zalessky, 2023. Slides (1,5 MB)

Row-permutable pairs of ODLS
Manzuk M.O., Vatutin E.I., Kochemazov S.E., Zaikin O.S. Interesting properties of orthogonal diagonal Latin squares of orders 7 and 8 (in Russian) // Recognition — 2017. Kursk: SWSU, 2017. P. 235–237. Download (198 KB)
Manzyuk M., Nikitina N., Vatutin E. Start-up and the Results of the Volunteer Computing Project RakeSearch // Communications in Computer and Information Science book series. Vol. 1129. Springer, 2019. pp. 725–734. DOI: 10.1007/978-3-030-36592-9_59. Download

Symmetries and automorphisms of DLS
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Titov V.S. Investigation of the properties of symmetric diagonal Latin squares (in Russian) // Proceedings of the 10th multiconference on control problems. Vol. 3. Rostov-on-Don, Taganrog, 2017. P. 17–19. Download (163 KB)
Vatutin E.I., Kochemazov S.E., Zaikin O.S. On Some Features of Symmetric Diagonal Latin Squares // CEUR Workshop Proceedings. Vol. 1940. Proceedings of the XIII International Scientific Conference on Optoelectronic Equipment and Devices in Systems of Pattern Recognition, Image and Symbol Information Processing. Aachen, Germany, 2017. pp. 74–79. Download (202 KB)
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Titov V.S. Investigation of the properties of symmetric diagonal Latin squares. Working on errors (in Russian) // Intellectual and Information Systems (Intellect – 2017). Tula, 2017. pp. 30–36. Download (167 КБ) Slides (1,0 MB)
Vatutin E.I., Zaikin O.S., Kochemazov S.E., Manzuk M.O. Program for getting symmetric diagonal Latin squares using Brute Force approach (in Russian) // Certificate of official registration of the computer software № 2018610493 from 11.01.2018.
Vatutin E.I., Zaikin O.S., Kochemazov S.E., Valyaev S.Y. Using Volunteer Computing to Study Some Features of Diagonal Latin Squares // Open Engineering. Vol. 7. Iss. 1. 2017. pp. 453–460. DOI: 10.1515/eng-2017-0052. Download
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Manzuk M.O., Nikitina N.N., Titov V.S. Properties of central symmetry for diagonal Latin squares (in Russian) // High-performance computing systems and technologies. No. 1 (8). 2018. pp. 74–78. Download (230 KB)
Vatutin E.I., Kochemazov S.E., Zaikin O.S., Manzuk M.O., Nikitina N.N., Titov V.S. Central Symmetry Properties for Diagonal Latin Squares // Problems of Information Technology. No. 2. 2019. pp. 3-8. DOI: 10.25045/jpit.v10.i2.01. Download (702 KB)
Vatutin E.I., Belyshev A.D., Zaikin O.S., Nikitina N.N., Manzuk M.O. Investigating of properties of generalized symmetries in diagonal Latin squares using volunteer distributed computing (in Russian) // High-performance computing systems and technologies. 2019. Vol. 3, No. 2. pp. 39–51. Download (414 KB)

Combinatorial structures of ODLS
Vatutin E.I., Titov V.S., Zaikin O.S., Kochemazov S.E., Manzuk M.O. An analysis of the combinatorial structures from the diagonal Latin squares of order 10 on the binary relation of orthogonality (in Russian) // Information technologies and mathematical modeling of a systems 2017. Moscow: Center of Information Technologies in Mathematical Modeling of RAS, 2017. pp. 167–170. Download (170 КБ)
Vatutin E.I. Investigation of symmetry properties during orthogonality-based classification of diagonal Latin squares of order 10 // Recognition — 2018. Plenary report. Slides (1,4 MB)
Vatutin E.I., Titov V.S., Zaikin O.S., Kochemazov S.E., Manzyuk M.O., Nikitina N.N. Orthogonality-based classification of diagonal Latin squares of order 10 // Distributed computing and grid-technologies in science and education (GRID’18): book of abstracts of the 8th international conference. Dubna: JINR, 2018. pp. 94–95. Download (16 KB)
Vatutin E.I., Titov V.S., Zaikin O.S., Kochemazov S.E., Manzuk M.O., Nikitina N.N. Orthogonality-based classification of diagonal Latin squares of order 10 // CEUR Workshop Proceedings. Vol. 2267. Proceedings of the VIII International Conference "Distributed Computing and Grid-technologies in Science and Education" (GRID 2018). Dubna, JINR, 2018. pp. 282–287. Download (410 KB)
Vatutin E.I., Manzuk M.O., Titov V.S., Kochemazov S.E., Belyshev A.D., Nikitina N.N. Orthogonality-based classification of diagonal Latin squares of orders 1–8 (in Russian) // High-performance computing systems and technologies. Vol. 3. No. 1. 2019. pp. 94–100. Download (299 KB)

Full list of the combinatorial structures from DLS of orders 1—8 on orthogonality relationship set (rus, eng).
Full list of the combinatorial structures from DLS of order 9 on orthogonality relationship set (rus, eng).
List of known combinatorial structures from DLS of order 10 on orthogonality relationship set (rus, eng).
List of known combinatorial structures from DLS of order 11 on orthogonality relationship set (rus, eng).

Cliques from ODLS
Vatutn E.I., Nikitina N.N., Manzuk M.O., Zaikin O.S., Belyshev A.D. Cliques properties from diagonal Latin squares of small order (in Russian) // Intellectual and Information Systems (Intellect – 2019). Tula, 2019. pp. 17–23. Download (167 КБ), Slides (1,4 MB)

Cell mapping schemes (CMS)
Vatutin E.I. Using cell mapping schemas during searching for pairs of orthogonal diagonal Latin squares // National supercomputing forum (NSCF — 2019). Slides (1,0 MB)
Vatutin E.I., Zaikin O.S., Manzuk M.O., Nikitina N.N. Searching for Orthogonal Latin Squares via Cells Mapping and BOINC-Based Cube-And-Conquer // Communications in Computer and Information Science. 2021. Vol. 1510. pp. 498–512. DOI: 10.1007/978-3-030-92864-3_38. Slides (1,5 МБ), Download
Vatutin E., Zaikin O. Classification of Cells Mapping Schemes Related to Orthogonal Diagonal Latin Squares of Small Order // Lecture Notes in Computer Science. Vol. 14389. Springer, Cham., 2023. pp. 21–34. DOI: 10.1007/978-3-031-49435-2_2. Download, Slides (1,0 MB)

Spectial types of LS/DLS
Vatutin E.I. Enumerating cyclic and pandiagonal Latin squares and their properties // National supercomputing forum (NSCF — 2020). Slides (665 KB)
Vatutin E.I. Enumerating cyclic Latin squares and Euler totient function calculatig using them (in Russian) // High-performance computing systems and technologies. 2020. Vol. 4. No. 2. pp. 40–48. Download (352 KB)
Vatutin E.I. Enumerating the Main Classes of Cyclic and Pandiagonal Latin Squares (in Russian) // Recognition — 2021. pp. 77–79. Slides (669 KB) Article (179 KB) Video
Vatutin E.I. Special types of diagonal Latin squares (in Russian) // Cloud and distributed computing systems in electronic control conference, within the National supercomputing forum (NSCF — 2022). Pereslavl-Zalessky, 2023. pp. 9–18. Download (453 KB), Slides (1,9 МБ) Video

Spectra of numerical characteristics of LS/DLS
Vatutin E.I., Nikitina N.N., Manzuk M.O., Albertyan A.M., Kurochkin I.I. On the construction of spectra of fast-computable numerical characteristics for diagonal Latin squares of small order // Intellectual and Information Systems (Intellect – 2021). Tula, 2021. pp. 7–17. Download (213 KB), Презентация (1,8 МБ)
Vatutin E.I. On the construction of spectra of numerical characteristics of diagonal Latin squares using volunteer computing // National supercomputing forum (NSCF — 2021). Slides (2,3 MB)
Vatutin E.I., Titov V.S., Pykhtin A.I., Kripachev A.V., Nikitina N.N., Manzuk M.O., Albertyan A.M., Kurochkin I.I. Estimation of the Cardinalities of the Spectra of Fast-computable Numerical Characteristics for Diagonal Latin Squares of Orders N>9 (in Russian) // Science and education in the development of industrial, social and economic spheres of Russian regions. Murom, 2022. pp. 314–315. Download (170 KB)
Vatutin E.I., Titov V.S., Pykhtin A.I., Kripachev A.V., Nikitina N.N., Manzuk M.O., Albertyan A.M., Kurochkin I.I. Heuristic method for getting approximations of spectra of numerical characteristics for diagonal Latin squares (in Russian) // Intellectual information systems: trends, problems, prospects. Kursk: SWSU, 2022. pp. 35–41. Download (423 KB)
Vatutin E.I., Nikitina N.N., Manzuk M.O., Kurochkin I.I., Albertyan A.M., Kripachev A.V., Pykhtin A.I. Methods for getting spectra of fast computable numerical characteristics of diagonal Latin squares (in Russian) // Cloud and distributed computing systems in electronic control conference, within the National supercomputing forum (NSCF — 2022). Pereslavl-Zalessky, 2023. pp. 19–23. Download (345 KB), Slides (963 KB) Video

Diagonalizing and canonizing of DLS
Vatutin E.I. Distributed diagonalization strategy for Latin squares (in Russian) // Science and education in the development of industrial, social and economic spheres of Russian regions. Murom, 2023. pp. 309-311. Download (168 KB)
Vatutin E., Belyshev A., Nikitina N., Manzuk M., Albertian A., Kurochkin I., Kripachev A., Pykhtin A. Diagonalization and Canonization of Latin Squares // Lecture Notes in Computer Science. Vol. 14389. Springer, Cham., 2023. pp. 48–61. DOI: 10.1007/978-3-031-49435-2_4. Download, Slides (1,6 MB)

Miscellaneous

Valyaev V.V., Vatutin E.I. Method for determining graph isomorphism at polinomial time (in Russian) // Proceedings of Southwest State University. Series: Control, Computer Science, Informatics. Medical Devices. № 2. Part 1. 2012. P. 200–206. Download (327 KB)
Vatutin E.I. Increasing differentiating ability of Randic index (in Russian) // Recognition – 2013. Kursk, 2013. P. 237–240. Download (199 KB)
Vatutin E.I., Valyaev V.V. The program for building supposing full polinomial invariant of graph and checking pair of graphs for isomorphism (in Russian) // Certificate of official registration of the computer software № 2013618656 from 13.09.13.
Vatutin E.I. The program for testing correctness of methods for graph isomorphism checking (in Russian) // Certificate of official registration of the computer software № 2013619188 from 26.09.13.
Vatutin E.I. The program for building classes of isomorphism and testing correctness of methods for graph isomorphism checking based on it (in Russian) // Certificate of official registration of the computer software № 2013619186 from 26.09.13.
Vatutin E.I., Titov V.S. Strategies for verifying correctness of methods for graph isomorphism checking using grid-systems (in Russian) // Proceedings of Southwest State University. 2014. № 1 (52). P. 26–30. Download (190 KB)
Vatutin E.I. An heuristic approach for graph isomorphism checking (in Russian) // Recognition – 2015. Kursk, 2015. P. 80–83. Download (192 KB) Video (begin)
Vatutin E.I., Titov V.S., Emelyanov S.G. Basics of discrete combinatorial optimization (in Russian). M.: Argamac-media, 2016. 270 p. ISBN 978-5-00024-057-1. Download (brief) (716 KB)

Main page | Cribs | Humor | For students

Last update: Jan 15 2024